Presentation
ACMP05 - Efficient, Portable, Massively Parallel Free-Space Solvers for the Poisson Equation
Presenter
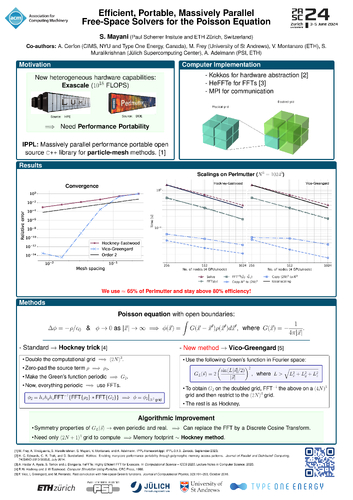
DescriptionVico et al. (2016) suggest a fast algorithm for computing volume potentials which is of benefit to the beam and plasma physics communities, as they require the solution of Poisson’s equation with free-space boundary conditions. The standard method to solve the free-space Poisson equation is to use the algorithm presented by Hockney and Eastwood (1988), which is second order in convergence at best. The algorithm proposed by Vico et al., which we refer to as Vico-Greengard, converges spectrally, i.e. faster than any fixed order of the number of grid points, for smooth enough functions. We implement a performance portable Poisson solver in the framework of the IPPL (Independent Parallel Particle Layer) library based on these two methods: the traditional Hockney-Eastwood, and the novel Vico-Greengard. Furthermore, we suggest an improvement to the Vico-Greengard algorithm which reduces its memory footprint. We show that for sufficiently smooth distribution functions, the Vico-Greengard algorithm could be a good candidate for reducing memory usage, since better accuracy can be obtained with a coarser grid. This is especially significant for GPUs, which present memory constraints. Finally, we showcase performance through scaling studies on the Perlmutter (NERSC) supercomputer, with efficiencies staying above 50% in the strong scaling case.
TimeTuesday, June 410:06 - 10:07 CEST
LocationHG F 30 Audi Max
Session Chair
Event Type
Poster